MEDIDAS DE ÁNGULOS

mayo 11, 2020

MEDIDAS DE ÁNGULOS

Definición

Para medir ángulos se utiliza el sistema sexagesimal.

Grado sexagesimal es la amplitud del ángulo resultante de dividir la circunferencia en 360 partes iguales.

Un grado tiene 60 minutos (') y un minuto tiene 60 segundos ('').

1º = 60' = 3600''

1' = 60''

Radianes

Otra unidad para medir ángulos es el radián.

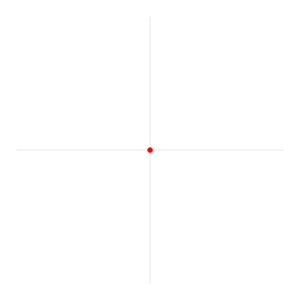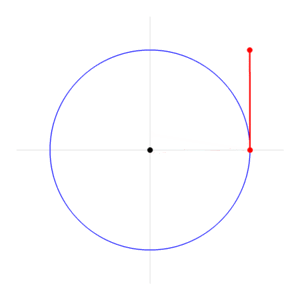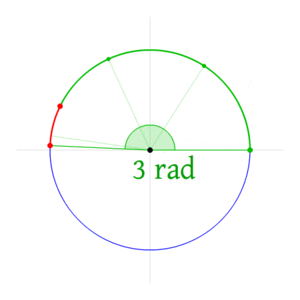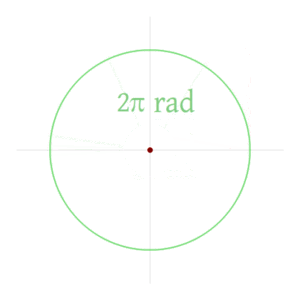
Un ángulo de 1 radián ocupa un arco de circunferencia de longitud su radio.
Una circunferencia completa tiene $2\pi$ radianes

1 rad= 57° 17' 44.8''
360º = 2rad
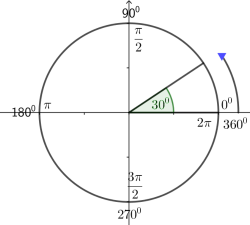
180º = rad
30º"=""> rad

/3 rad "=""> º

Convertir entre grados y radianes

Para convertir entre grados y radianes usamos la equivalencia 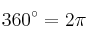$360^{\circ} =2 \pi$ radianes, o mejor incluso

$180^{\circ} = \pi$ radianes

Por tanto, con una simple "regla de tres" podemos transformar grados en radianes y viceversa.

Ejemplo: ¿Cuántos radianes son 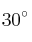$30^{\circ}$ ?

$180^{\circ} \longrightarrow \pi \: rad$
$\: 30^{\circ} \longrightarrow x \: rad$

$x = \frac{30 \cdot \pi}{180}= \frac{30 \pi}{180}=\frac{\pi}{6} \: rad$

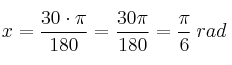
2- Sistema sexagesimal

El sistema sexagesimal es un sistema de unidades muy empleado cuyo fundamento es que cada unidad se divide en 60 unidades de una orden inferior, es decir, es un sistema de numeración en base 60.

A su vez, cada grado se subdivide en otras unidades inferiores, en concreto, en sesenta partes iguales. De esta manera, cada grado se divide en 60 minutos (1º = 60´) y cada minuto, a su vez, en 60 segundos (1´ = 60´´).

• Medidas de ángulos: 1 grado (º) → 60 minutos (´) → 60 segundos (´´)

• Medidas de tiempo: 1 hora → 60 minutos (´) → 60 segundos (´´)

Por tanto, en general, un ángulo en el sistema sexagesimal vendrá expresado en grados, minutos y segundos, de la forma, por ejemplo: 38º 50´ 35´´ (38 grados, 50 minutos y 35 segundos). Si se omiten los minutos y segundos, por ejemplo, 45º, es porque se entiende que es 45º 0´ 0´´.

Cuando un ángulo se mide en grados, minutos y segundos, se dice que está expresado con medida compleja, mientras que si se expresa con una sola clase de unidades, se dice que es una medida incompleja o simple, por ejemplo:

32º → medida simple

11´´ → medida simple

52º 17´ 45´´ → medida compleja

4º 22´ → medida compleja

Para sumar grados expresados en medidas complejas, primero se colocan los grados debajo de los grados, los minutos debajo de los minutos y los segundos debajo de los segundos, y se suman, como se indica en el siguiente ejemplo de la figura:

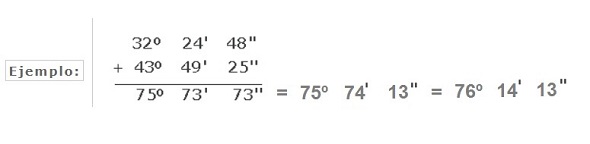
3- Sistema centesimal

El sistema centesimal divide una circunferencia en 400 partes iguales, o bien, un ángulo recto en 100 partes iguales, y a cada una de esas partes se le denomina grado centesimal o gradián, y se simboliza con una «g» minúscula como superíndice del número, por ejemplo 35^g.

A su vez, cada grado centesimal se subdivide en unidades más pequeñas dividiéndolo en cien partes iguales, y dando lugar al minuto. Así, el minuto (m) en este sistema es la centésima parte del grado (1g = 100m) y el segundo (s) la centésima parte del minuto (1m = 100s).

De la misma manera, el segundo se divide en décimas, centésimas, milésimas,... Un ejemplo de un ángulo expresado según el sistema centesimal sería: 40g 30m 10s.

Por otro lado, el método para expresar en forma decimal un grado expresado en minutos y segundos centesimales es muy sencillo, ya que basta con colocar una coma después de los grados, así 40^g 30^m 10^s = 40,3010g.

Y la conversión inversa, es decir, para pasar de grados centesimales en forma decimal a minutos y segundos centesimales se realiza como se indica en el siguiente ejemplo:

- Pasar 26,2547g a grados minutos y segundos centesimales

26,2547g = 26g + 0,25 · 100 + 0,0047 · 10000 = 26g + 25m + 47s

MEDIDAS DE ÁNGULOS