RAZONES TRIGONOMÉTRICAS

El origen etimológico de las dos palabras que le dan forma son:

-Razones deriva del latín, de “ratio”, que es sinónimo de “razón”.

-Trigonométrico, por su parte, tiene un origen griego. Significa “relativo a la trigonometría”, y está compuesta de los siguientes elementos de esa lengua: el sustantivo “trigonon”, que puede traducirse como “triángulo”; el nombre “metron”, que equivale a “medida”, y el sufijo “-ico”, que significa “relativo a”.

Las razones trigonométricas de un ángulo α son las razones obtenidas entre los tres lados de un triángulo rectángulo. Es decir, la comparación por su cociente de sus tres lados a, b y c.

• El seno de un ángulo α se define como la razón entre el cateto opuesto (a) y la hipotenusa (c).

Sea α uno de los ángulos agudos del triángulo rectángulo.

• El coseno se define como la razón entre el cateto contiguo o cateto adyacente (b) y la hipotenusa (c).

• La tangente es la razón entre el cateto opuesto (a) y el cateto contiguo o cateto adyacente (b).

Razones trigonométricas de ángulos característicos

El seno, coseno y tangente de los ángulos más característicos (0º, 30º, 45º, 60º, 90º, 180º y 270º) son:

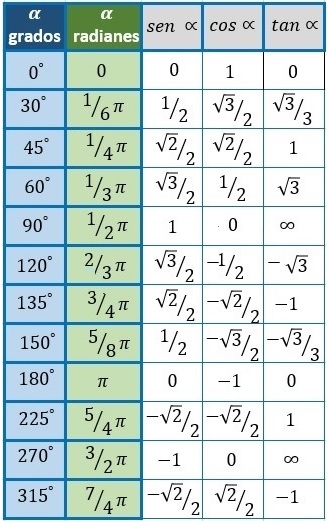
Relación entre razones trigonométricas

Cualquier razón trigonométrica se puede expresar en función de cualquier otra. En la siguiente tabla se puede ver la fórmula con la que se expresa cada una en función de la otra.

Nota: el signo ± que corresponde en cada caso depende del cuadrante en que esté el ángulo.

Razones trigonométricas del ángulo complementario

• Seno del ángulo complementario:

• Coseno del ángulo complementario:

• Tangente del ángulo complementario:

Razones trigonométricas del ángulo suplementario

• Seno del ángulo suplementario:

• Coseno del ángulo suplementario:

• Tangente del ángulo suplementario:

Razones trigonométricas del ángulo conjugado

• Seno del ángulo conjugado:

• Coseno del ángulo conjugado:

• Tangente del ángulo conjugado:

Razones trigonométricas del ángulo opuesto

• Seno del ángulo opuesto:

• Coseno del ángulo opuesto:

• Tangente del ángulo opuesto:

Razones trigonométricas del ángulo que difiere 90º

• Seno del ángulo que difiere 90º:

• Coseno del ángulo que difiere 90º:

• Tangente del ángulo que difiere 90º:

Razones trigonométricas del ángulo que difiere 180º

• Seno del ángulo que difiere 180º:

• Coseno del ángulo que difiere 180º:

• Tangente del ángulo que difiere 180º:

Razones trigonométricas del ángulo suma

• Seno del ángulo suma:

• Coseno del ángulo suma:

• Tangente del ángulo suma:

Razones trigonométricas del ángulo resta

• Seno del ángulo resta:

• Coseno del ángulo resta:

• Tangente del ángulo resta:

Razones trigonométricas del ángulo doble

• Seno del ángulo doble:

• Coseno del ángulo doble:

• Tangente del ángulo doble:

Razones trigonométricas del ángulo mitad

• Seno del ángulo mitad:

• Coseno del ángulo mitad:

• Tangente del ángulo mitad:

Razones trigonométricas del ángulo triple

• Seno del ángulo triple:

• Coseno del ángulo triple:

• Tangente del ángulo triple:

Razones trigonométricas recíprocas de α

• Cosecante de α:

• Secante de α:

• Cotangente de α:

Funciones trigonométricas inversas

Las funciones trigonométricas inversas se definen como las inversas de las razones trigonométricas.

Son funciones trigonométricas inversas: arcoseno, arcocoseno y arcotangente.

Funciones trigonométricas

• Se pueden representar gráficamente las razones y las razones inversas en el triángulo sobre una circunferencia de radio r=1.